How about some sort of Euclidean generator and something similar to the Turing machine.
Agra that would be awesome stuff to have
If I would ask you to explain the benefit of such a feature to me, in simple words, how would you do that?
Euclidean algo is great for “exotic” rhythms. Combining several of these can make pretty complicated poly rhythm style music. Like rhythm found in African style music among a lot of other exotic rhythm styles.
What it basically does is distribute the amount of wanted hits as evenly as possible according to the length you want.
So if you for example say you want 4 hits on a 16 step sequencer it would be:
X 2 3 4 X 6 7 8 X 10 11 12 X 14 15 16
(X are the 4 hits that will be played back)
That’s pretty simple, cause 16 can be divided by 4, so they steps will be distributed as 1/4 notes.
Another more exotic example, if you want 6 hits on a 13 step sequence:
X 2 3 X 5 X 7 X 9 X 11 X 13
(X are the 6 hits that will be played back)
This is a bit more exotic rhythm.
Anyway, I hope you get the idea ![]()
There are lots of papers, explanations on Youtube on the web if you want to dig more into it.
For example:
It’s really simple to make in Pure Data. Google a bit, there are many patches, IIRC also a turing machine style euclidean sequencer.
Turing machine shifts bits left and then runs them through a DAC, randomly flipping the least significant bit.
It might be fractal, but it’s not euclidean.
I know, but that’s what many people call these types of sequencers.
My point was not really about what was the correct term, my point was that someone already made it for PD ![]()
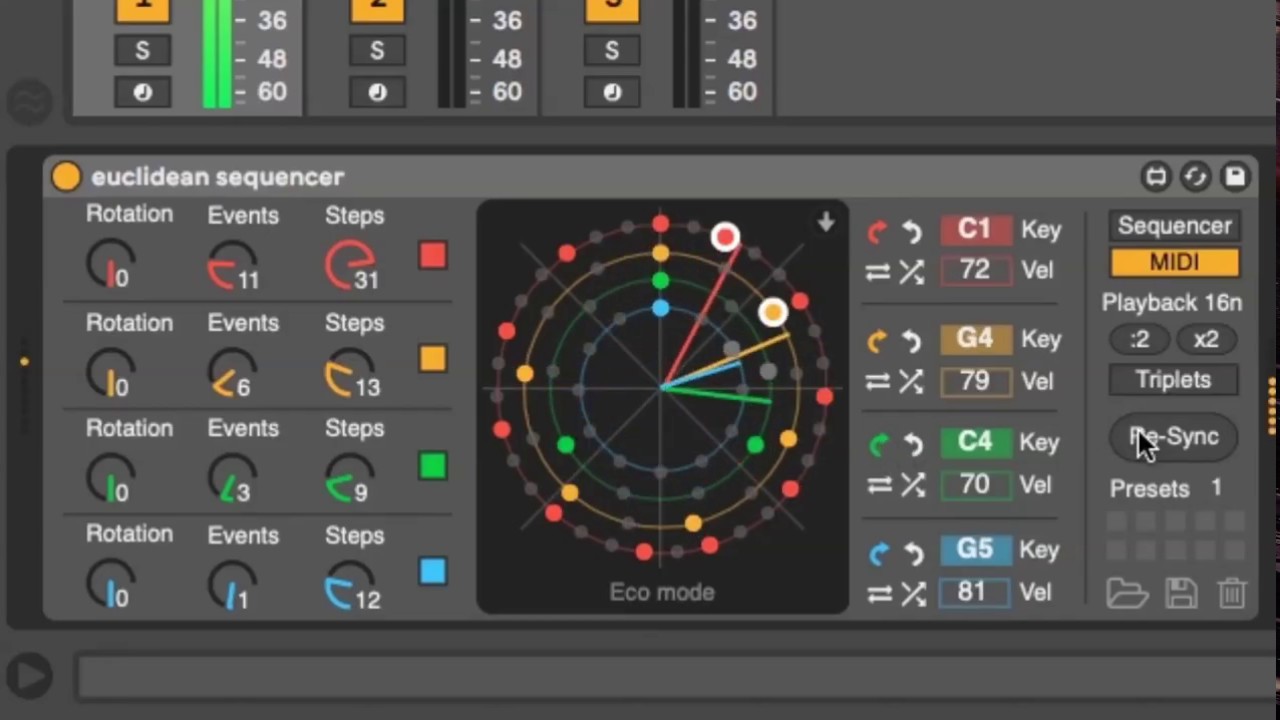
the LXR-02 has a great implementation of the euclidean algorithm. just three values: length (the number of steps in the pattern), step (the number of steps to be distributed as equally as possible within the pattern), and rotate (where you can move the resulting pattern forward or backward a step in time). it’s very valuable for creating beats: almost all standard rhythms are variations of the algorithm-- after generation you then add or subtract beats to taste, of course. it might be a great set of extra options on the arpeggiator?
A euclidean generator would still be great to have ![]()
I find myself comfortable using Orca for this purpose. Works very well as a computer assisted addition to the midihub (great tip in my opinion, love me for this).
I wonder if some genius might have implemented Euclidean using existing pipelines. Do you think it’s possible?
It is not that difficult, did you know why it is called euclidean ? Hahaha
A quick and dirty way to do it would be to set different clock division manually.
- If you have 16 steps for 1 bar as reference you have a ration 16/16=1 at, for exemple, 120 bpm, it is 120 x 1 = 120 bpm
- So if you want a not so fancy 8 steps over 16 you will have an other ratio 8/16=0,5… so 120 x 0,5 = 60 bpm
- If you want a really fancy 14 steps over 16 (14 / 16 x 120) use 105 bpm
- If you a nearly too fancy 5 steps over 16 (5 / 16 x 120) use 37,5 bpm
Now feed each clock to delay and / or a arp pipes
- For delays set repetition to the number of steps your bpm is set for (and and maybe some randomness and and « remap » scale quantification)
- For arps feed with chords (maybe with harmony and remap scale quantification pipes) with as much note as number of steps your bpm is set for (add randomness here too !)
Note that euclidean is polyrhythm, if, for example, you use more or less notes in your chords to feed your arp pipe than the number of steps your bpm is set for, you will get polymeter on top of polyrhythm., witch could be messy or beautiful depending on what you try to achieve.
@Giedrius since this if one of the most voted feature, and since euclidean is so hype today (every big sequencer add euclidean and polymeters on there updates for two or three years now ^^)
I would suggest you to add euclidean ratio to enable euclidean generative patch !
If I had to implement that feature I would add, under classic division selection, a euclidean division part where users can enter how many division they want.
For exemple entering 16 steps (4 x 3) would gives us 16 ratio to use :
- 1/16 (,0625)
- 2/16 (,125)
- 3/16 (,1875)
- 4/16 (,25)
- 5/16 (,3125)
- …
Entering 12 steps (4 x 3) gives us 12 ratio to use… entering 11 steps…
It could be called euclidean ratio and could be added everywhere time ratio is already implemented.
The ratio selection must be mappable to be fair and fun ![]()
I am working daily with an euclidean sequencer (torso t-1) and it is amazing to work with. If you need beta testing or whatever I would be happy to provide it ![]()
hey, Nathan, would you post up a patch for this?
I can ! I’m out for some days right now, but I add it on my To-Do list ![]()
Looking forward to this!
Thanks to Nathan @jazzstang for bumping this up the listings again, not least because I’d missed @eiccolor’s post in December:
Orca
Very grateful for the mention of Orca which looks a bonkers PacMan For MIDI!
(for those like me who nothing about it this video jumps straight in with some live patching)
@eiccolor once you’re comfortable with the syntax, Orca would be a lightweight way to do Euclidean patterns.
PS @Blokas, I wonder whether this could be a cool addition to PatchBox?
Euclidean for Midihub
@Claire_Upz, after a brief chat with via PM, I think @jazzstang’s strategies are more about polyrhythms than Euclidean rhythms per se; I’m looking forward to a patch to find out for sure.
It got me thinking about this
did some reading...
the original paper is worth it:
http://cgm.cs.mcgill.ca/~godfried/publications/banff.pdf (gives a warning on some browser but) its a good read.
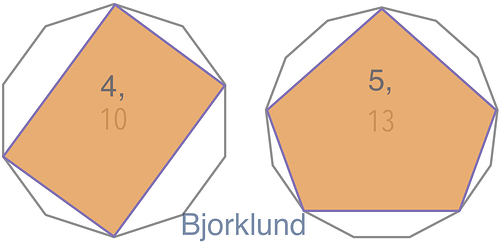
Brian House’s Bjorklund Python script is an easy way to generate any beats per steps pattern.
Btw He..
…found many implementations of the algorithm in various languages…return inaccurate results
So sound like there are some shaky algorithms out there.
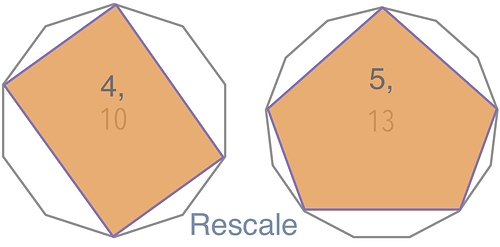
If you see Euclid/Björklund as just a way of getting “the most equal spread of b beats in s steps” then Midihub’s Rescale can do the job. It does the same job another way.
compare:
with:
So, yes @eiccolor, I think it’s possible, depending what “it” is:
It’s got me thinking about a thing involving a Synced LFO (mapped depth) going to a Rescale (& then, I think, a Dispatcher).
This will run, say, 5beats in 13 where the whole cycle will repeat at say 1bar at 60BPM (=4 secs)
Only time and testing will tell how usable it’ll be.
Thanks @resonotter for your input, my guess is that polyrhythm is part of the fun of using Euclidean generators. The magic happens when you run two conflicting Euclidean generated voices where steps and notes number don’t match between voices but loop in a same amount of time.
But Polyrhythms, Polymeters and Euclidean Rhythm could be confusing terms to use and sometimes refer more to an « undefined groovy magical rhythm » ^^
To start, let’s differentiate between polyrhythms and polymeters:
Polymeters involve two conflicting voices, where the step count resets at a fixed but different step number for each voice. For example, a 3 against 4 polymeter would look like this:
Voice 1: 123 123 123 123
Voice 2: 123 412 341 234
To me Polymeters are not part of what we call Euclidean Rythms.
Polyrhythms, on the other hand, involve two conflicting voices with different numbers of steps in the same amount of time. For instance, a 3 against 4 polyrhythm would look like this:
Voice 1: 1 2 3 1 2 3
Voice 2: 1 2 3 4 1 2 3 4
Now, let’s discuss Euclidean rhythm generators, and what I think we refer to when using this term.
An Euclidean rhythm generator utilizes an algorithm to evenly distribute notes over a fixed number of steps. To replicate this, you can have a voice with x notes on y steps, where y equals x (each step is filled with a note), over z steps where z is not equal to x. Then, quantize or rescale x notes over z steps.
An Euclidean rhythm generator typically requires the following parameters:
- Number of steps
- Number of notes
- Rotation parameter (to rotate the geometrical shape)
Adding a second voice with a different number of steps results in polyrhythms. However, the way notes are filled over the steps still employs the Euclidean algorithm.
In conclusion, while we can mimic the results of an Euclidean Rhythm Generator using midihub, we may miss out on the enjoyable aspects of easy controls and happy accidents that come with using an actual generator.
That’s why, to me, the best use case of a Euclidean Generator in Midihub could be an arpegiator, inputting a chord as note pool, having control on the number of notes, of steps using subdivision (a against b) and rotation, having typical arpegiator controls over notes.
Here is a small C++ code I was working on years ago. It prompt for numbers of voices, steps, notes, rotation and bpm, and output midi 60 (C3) notes on channel 1 to 16 depending on the number of voices you need. It might be buggy, I don’t run it for a long time, but the I guess the interesting part is the use of vector.
#include <iostream>
#include <vector>
#include <rtmidi/RtMidi.h>
#include <thread>
#include <mutex>
#include <condition_variable>
std::mutex mtx;
std::condition_variable cv;
bool clockReceived = false;
double bpm = 120.0; // Default BPM
// MIDI Output function
void sendMidiMessages(RtMidiOut& midiOut, int channel, int note) {
try {
std::vector<unsigned char> message(3);
message[0] = 0x90 | channel; // Note on event on the specified channel
message[1] = note; // Note number (C3)
message[2] = 100; // Velocity
midiOut.sendMessage(&message);
} catch (RtMidiError& error) {
std::cerr << "Error: " << error.getMessage() << std::endl;
}
}
// Function to generate Euclidean rhythm
std::vector<bool> generateEuclideanRhythm(int steps, int notes, int rotation) {
std::vector<bool> rhythm(steps, false);
if (notes <= 0 || steps <= 0 || notes > steps)
return rhythm;
std::vector<int> pattern;
int remainder = steps - notes;
int divisor = notes;
// Generate Euclidean rhythm pattern
while (divisor != 0) {
pattern.push_back(remainder / divisor + 1);
remainder %= divisor;
divisor--;
}
// Rotate the pattern based on the rotation parameter
std::rotate(pattern.begin(), pattern.begin() + rotation, pattern.end());
// Apply the pattern to the rhythm
int index = 0;
for (int i = 0; i < pattern.size(); ++i) {
for (int j = 0; j < pattern[i]; ++j) {
rhythm[index] = true;
index = (index + 1) % steps;
}
}
return rhythm;
}
// Function to handle MIDI clock events
void midiClockHandler(double deltatime, std::vector<unsigned char> *message, void *userData) {
clockReceived = true;
cv.notify_one();
}
int main() {
RtMidiIn midiIn;
RtMidiOut midiOut;
int numVoices;
// Prompt for the number of voices
std::cout << "Enter number of voices (up to 16): ";
std::cin >> numVoices;
// Open MIDI ports
try {
midiIn.openVirtualPort("EuclideanRhythmIn");
midiOut.openVirtualPort("EuclideanRhythmOut");
} catch (RtMidiError &error) {
std::cerr << "Error: " << error.getMessage() << std::endl;
return 1;
}
// Set up MIDI clock input
midiIn.setCallback(&midiClockHandler);
// Wait for MIDI clock or prompt for BPM
std::unique_lock<std::mutex> lock(mtx);
cv.wait(lock, [] { return clockReceived; });
// Prompt for BPM if MIDI clock is not received
if (!clockReceived) {
std::cout << "MIDI clock not detected. Enter BPM: ";
std::cin >> bpm;
}
// Clear MIDI clock callback
midiIn.cancelCallback();
// Generate rhythms and send MIDI messages for each voice
for (int i = 0; i < numVoices; ++i) {
int steps, notes, rotation;
std::cout << "\nVoice " << i + 1 << ":\n";
std::cout << "Enter number of steps (1-16): ";
std::cin >> steps;
std::cout << "Enter number of notes (1-" << steps << "): ";
std::cin >> notes;
std::cout << "Enter rotation (1-" << steps << "): ";
std::cin >> rotation;
// Generate Euclidean rhythm
std::vector<bool> rhythm = generateEuclideanRhythm(steps, notes, rotation);
// Send MIDI messages for the voice
std::thread voiceThread([&]() {
int channel = i + 1; // MIDI channel (1 to 16)
for (bool beat : rhythm) {
if (beat) {
sendMidiMessages(midiOut, channel - 1, 60); // Send C3 note
}
std::this_thread::sleep_for(std::chrono::milliseconds(static_cast<int>((60000.0 / bpm) / steps))); // Adjust timing based on BPM
}
});
voiceThread.detach(); // Detach thread to run independently
}
// Wait for user input to exit
std::cout << "Press Enter to exit..." << std::endl;
std::cin.ignore(); // Ignore previous newline
std::cin.get();
// Cleanup
midiIn.closePort();
midiOut.closePort();
return 0;
}
Hey, @jazzstang,
Thanks for that.
best use case of a Euclidean Generator in Midihub could be an arpeggiator,
Good idea. There are a bunch of Rhythm pattern ideas it would be fun to see MH acquire.
In the meantime, I’m intrigued enough to explore Euclidean using existing firmware just to see how usable it could be made. Doing it in a fixed form is easy enough (but where’s the fun in that?)
So far I’ve got my b beats in s steps (1 < s < 33).
(Don’t have the rotations, leaving that for a bit)
Think I’ve got room for at least two Rhythms.
Want to have the option of playing the dots in [x . . x . x . . x . x .] as well as the x’s
I was going to just have them as spaces..
but then I noticed Toussaint saying
[x . . x . . x . . x . .] is the (12/8)-time Fandango clapping pattern in the Flamenco music of southern Spain, where ‘x’ denotes a loud clap and ‘.’ a soft clap
so I figured I might as well Transform them in to Poly Aftertouch; leaving later pipelines to either ditch them or use them.
Latest aspect to exercise me is “what to play?”. Don’t want to leave it hardwired once MH is stand-alone.
This is the current concept:
Nice thing about this is that, for every one of the 4 setting actions (which beat, what note, what octave, and what velocity ppp → fff), the corresponding note gets set again. This is cool cos then a note can be ‘copied’ from say beat 1 to beat 5 just by doing that one next. It all gets pretty meta though… (never had mappings deciding mappings before)